Option Pricing with the Black-Scholes-Merton Model
Below is more details of Black-Scholes-Merton Model:
The Black-Scholes-Merton Model is like the holy grail of option pricing. It's a fancy way to figure out how much an option should cost, and it's pretty realistic too. The cool thing is that it gives you a nice, neat solution that you can use.
So, the formula is actually a combination of two ideas from two papers one by Black and Scholes (1973) and another by Merton (1973). If you're interested in digging deeper into the details, you can check out their papers.
The model itself is made up of two separate equations. One is for pricing a call option, and the other is for pricing a put option.
Here's the formula for pricing a call option:
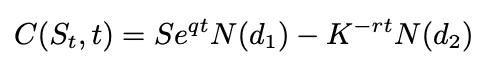
and Here's the formula for pricing a put option:
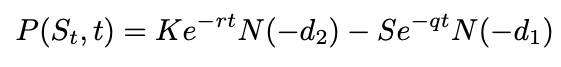
where N(x) is the standard normal cumulative distribution function:
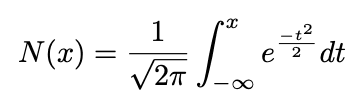
and
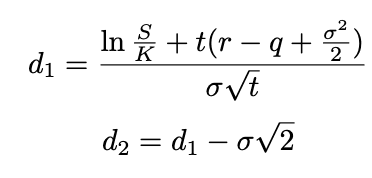
The parameters for the model is defined as follows:
- S = Underlying price
- K = Strike price
- σ = Volatility
- r = Constinously compounded risk-free rate
- q = Continuously compounded dividend yield (holding cost)
- t = Time to expiration
The formulas and parameters as stated in python are below:
from scipy.stats import norm
import math
def call_option_price(S, K, r, q , T, sigma):
d1 = (math.log(S / K) + (r-q + 0.5 * sigma**2) * T) / (sigma * math.sqrt(T))
d2 = d1 - sigma * math.sqrt(T)
call_price = S*math.exp(-q*T) * norm.cdf(d1) - math.exp(-r * T) * K * norm.cdf(d2)
return call_price
def put_option_price(S, K, r, q , T, sigma):
d1 = (math.log(S / K) + (r-q + 0.5 * sigma**2) * T) / (sigma * math.sqrt(T))
d2 = d1 - sigma * math.sqrt(T)
call_price = K*math.exp(-r*T)*N(-d2)-S*math.exp(-q*T)*N(-d1)
return call_price
Alright, let's chat about how we built this awesome calculator! So, first things first, I rolled up my sleeves and fired up Python to get things going. I created a super cool API using Django Rest Framework. It's like a magic wand that allows me to access the model in a snap.
Now, when it comes to the frontend stuff, what you're currently seeing is all thanks to NextJS. It's a nifty framework for building web pages with React. It makes things smooth and snappy, so you're in for a treat!
Now, let's talk about calculating the years to maturity. We decided to keep it simple and assume a 365-day calendar year. So, if you want to figure out how much time is left for an option to expire, we use 365 days as the total. But hey, we like to give you options! If you prefer a different number of days for your calendar, we got you covered. You can simply input your own value and customize the calculation to match your style.
